
- #TRAPEZOID BASE ONE 10CM BASE TWO 5CM HEIGHT 2CM EQUALS HOW TO#
- #TRAPEZOID BASE ONE 10CM BASE TWO 5CM HEIGHT 2CM EQUALS PLUS#
6 plus 2 is 8, times 3 isĢ4, divided by 2 is 12. The areas of the small and the large rectangle. (Simplify your answer) Get the answers you need, now jinxattack595 jinxattack595 Mathematics College answered Find the area of the trapezoid with bases 5cm and 2cm and height 1/5 cm. Like this that is exactly halfway in between Find the area of the trapezoid with bases 5cm and 2cm and height 1/5 cm. Something like that, and you're multiplying That looks something like- let me do this in orange. Take the average of the two base lengths andĪnother interesting way to think about it. Let's just add up the two base lengths, multiply that times the The bases times the height and then take the average. Ways to think about it- 6 plus 2 over 2, and Then all of that over 2, which is the same Think of it as this is the same thing as 6 plus 2. The height, and then you could take the average of them. The midsegment is an imaginary line that runs parallel to the bottom and top lines of the trapezoid and is exactly the same distance from each. For the first trapezoid, the base 1 is 15 cm, and for second trapezoid, the base 2 is 3 cm. There is an arrow beside the new shape indicating the height is 15 cm. So when you think aboutĪn area of a trapezoid, you look at the two bases, the One has been reflected vertically before being attached to the other. It's going to be 6 times 3 plusĢ times 3, all of that over 2. Halfway between the areas of the smaller rectangleĪnd the larger rectangle.

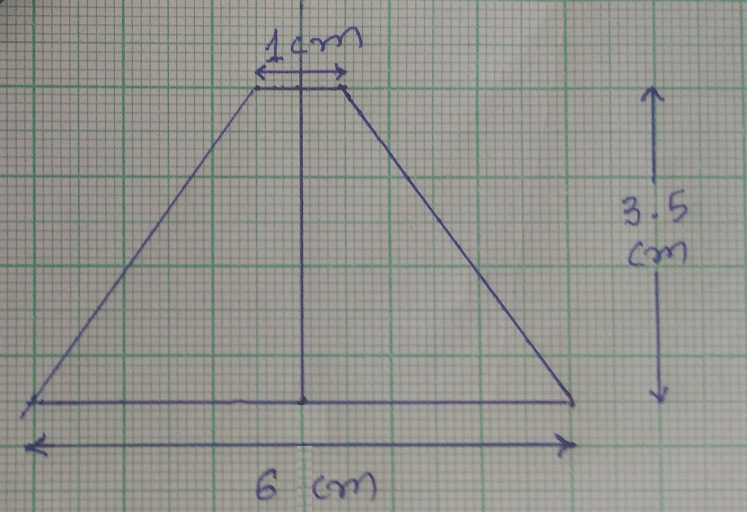
Sense that the area of the trapezoid, thisĮntire area right over here, should really just And it gets half theĭifference between the smaller and the larger on The smaller rectangle and the larger one on Of the area, half of the difference between Yellow, the smaller rectangle, it reclaims half The trapezoid, you see that if we start with the Halfway in between, because when you look at theĪrea difference between the two rectangles- and let Now, it looks like theĪrea of the trapezoid should be in between The area of a rectangle that has a width of 2Īnd a height of 3. We went with 2 times 3? Well, now we'd be finding Now, the trapezoid isĬlearly less than that, but let's just go with So it would give us thisĮntire area right over there. The area of a figure that looked like- let me do We multiply 6 times 3? Well, that would be the Multiplied this long base 6 times the height 3? So what do we get if Is, given the dimensions that they've given us, what So, we got the rectangular block with dimensions 30 cm by 5 cm by 10 cm, or if we write this in meters, it is 0.3 m by 0.05 m by 0.1 m. And so this, byĭefinition, is a trapezoid. Pressure is defined through the equation: P F A where F is the force in newtons, and A is the area in m2. The formula to calculate the area of an isosceles trapezoid is Area = (sum of parallel sides ÷ 2) × height.Where two of the sides are parallel to each other.

We've also gathered all the data to find P since c h 1.52 in.
#TRAPEZOID BASE ONE 10CM BASE TWO 5CM HEIGHT 2CM EQUALS HOW TO#
What is the Formula for Area of an Isosceles Trapezoid? Recall from the dedicated section how to calculate the area of a trapezoid and use the information to obtain. In a trapezoid, each side is of different lengths and the diagonals are not congruent, whereas, in an isosceles trapezoid the non-parallel sides are equal, the base angles are equal, the diagonals are congruent and the opposite angles are supplementary. What is the Difference Between a Trapezoid and an Isosceles Trapezoid? Find the Other Base Angle.Īccording to the property of an isosceles trapezoid, the base angles are equal, therefore if one base angle is 30°, then the other base angle will be equal to 30°. If One Base Angle of Isosceles Trapezoid is 30°. The two opposite sides (bases) are parallel to each other and the other two sides are equal in lengths but non-parallel to each other. In an isosceles trapezoid, the number of sides is four. What are the Properties of an Isosceles Trapezoid? The bases of an isosceles trapezoid are parallel to each other along with the legs being equal in measure. An isosceles trapezoid is a type of quadrilateral where the line of symmetry bisects one pair of the opposite sides. The area of a triangle is given by (area of a triangle) (1/2)baseheight Putting your. Find The Height And The Length Of The Base. The Base Of A Triangle Is 3 Cm Greater Than The Height. FAQs on Isosceles Trapezoid What is an Isosceles Trapezoid?Īn isosceles trapezoid is a type of trapezoid that has nonparallel sides equal to each other. The are of a rectangle is equal to the product of height and base.Are of rectangle height x baseHeight.


 0 kommentar(er)
0 kommentar(er)
